A Hierarchical Evaluation Metric for Document Classification
This blog post serves as an introduction to the methods described in the paper CoPHE: A Count-Preserving Hierarchical Evaluation Metric in Large-Scale Multi-Label Text Classification [1] presented at EMNLP 2021. For a more detailed description, along with comparison against previous evaluation metrics in this setting, please refer to the full publication.
Motivation
Evaluation in Large-Scale Multi-Label Text Classification, such as automated ICD-9 coding of discharge summaries in MIMIC-III [2], is treated in prior art as exact-match evaluation on the code level. Labelling is carried out on the document level (weak labelling), with each code appearing at most once per document. Hence, the prediction and gold standard for a document can be viewed as sets. The label space of MIMIC-III consists of leaf nodes within the ICD-9 tree (example substructure in Figure 1), treating both the prediction and the gold standard as flat (disregarding the ontological structure).
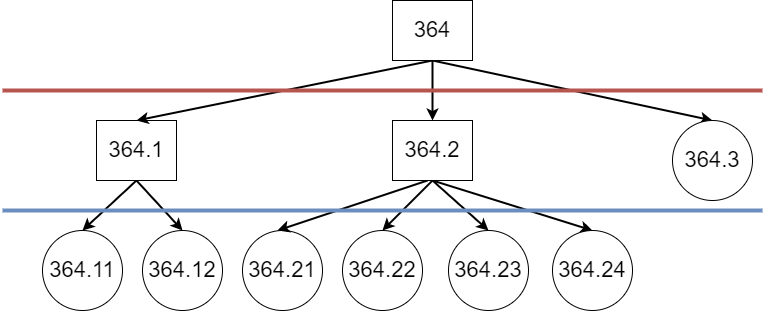
Within a structured label space, the concept of distance between labels naturally arises. If, for instance, we consider each edge within the ontology to be of equal weight, the code 410.01 Acute myocardial infarction of anterolateral wall, initial episode of care is closer to its sibling code 410.02 Acute myocardial infarction of anterolateral wall, subsequent episode of care than to a cousin code 410.11 Acute myocardial infarction of other anterior wall, initial episode of care, or a more distantly related code, e.g., 401.9 Unspecified essential hypertension. The standard flat evaluation does not capture this, and if the code 410.01 was mispredicted for a document to be any other code, through the standard flat exact-match approach the errors would be considered equivalent, disregarding the closeness of predictions to the gold standard.
Previous work has incorporated the structural nature of the label space of ICD ontologies, such as [3]. This study, however, concerns a different task – information extraction with strong labels. The ICD codes are assigned to specific spans of texts within the document. This strong labelling allows for associating a prediction to a gold standard label, and exact comparison on a case-by-case basis. This is, unfortunately, not possible in the weakly-labelled scenario of document-level ICD coding, where if a label is mispredicted we cannot state its corresponding gold standard label with certainty.
One of the approaches to creating a metric for the structured label space in [3] is tracing the distance between the closest common parent on the graph of the ontology (tree) and either of the prediction and the gold standard. We are unable to reuse this method exactly, lacking the knowledge of which gold standard codes relate to mispredictions. Instead, we are able to make use of the common ancestor.
Hierarchical Evaluation
One way to approach hierarchical evaluation in a weakly-labelled scenario is to not only evaluate on the leaf-level prediction, but also the codes’ ancestors. We can convert leaf-level predictions into ancestor predictions (e.g., by means of adjacency matrices,) and compare those against their respective converted gold standard (Figure 2). The core idea here is that codes appearing closer together within the ontology will share more ancestors, thereby mitigating the error that arises from misclassification.
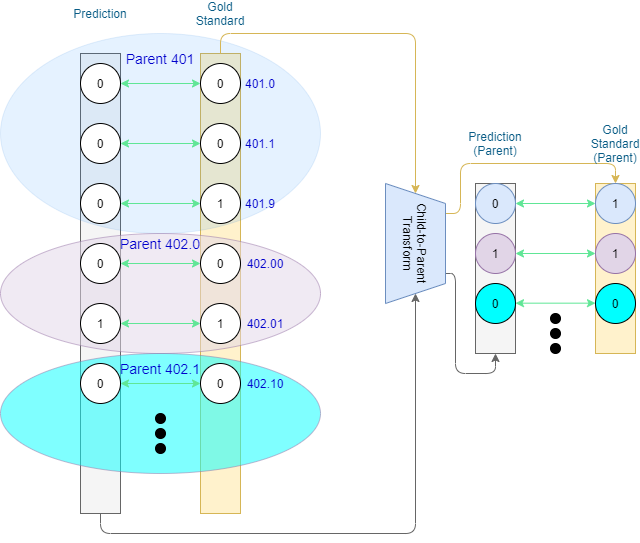
Once we have the ancestor-level values we can either report separate metrics for each level of the ontology, or a single metric on the combined information from different levels.
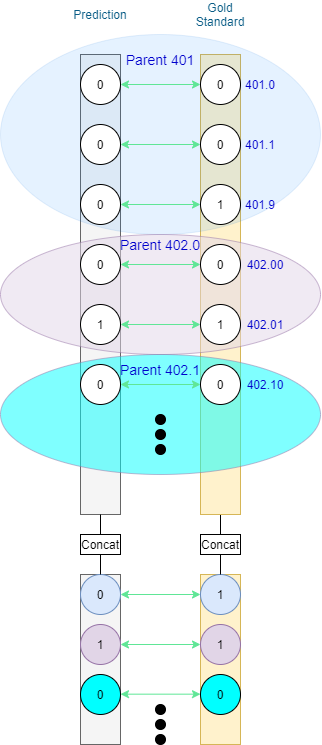
As prediction-level codes in MIMIC-III appear at different depths (as seen in Figure 1), it is reasonable to report performance based on different depths of the ontology. Depending on the implementation of the transition procedure, duplicates may appear.
The example presented in Figure 3 is neat in that at most one prediction is made for each of the shown code families on the leaf level. What about multiple predictions within the same family? One option would be to stick to binary as on the prediction level. If at least 1 prediction-level node within the family is positive, the family is considered to be positive (1), and negative (0) otherwise. As such, the value of ancestor nodes is the result of the logical OR operation on their descendants. Standard P/R/F1 can be applied for evaluation without further need for processing. Such an approach to hierarchical evaluation in multi-label classification was presented by Kosmopoulos et al. [4]
Count-Preserving Hierarchical Evaluation (CoPHE)
Alternatively, we can extend to full counts, in which case each family value is a sum of the values of the family’s prediction-level codes. This results in ancestor values in the domain of natural numbers. Standard binary P/R/F1 do not work in this case (as TP, FP, and FN are defined for binary input), but we retain more information that can tell us of over- or under-prediction for the ancestor codes. Why is this important? The ontology may contain inexplicit rules, such some code families allowing only a single code assigned per document – e.g., 401 (Essential Hypertension) has three descendant codes corresponding to malignant, benign, and unspecified hypertension respectively. From a logical standpoint, hypertension can be either malignant or benign, but not both at the same time, and would be considered unspecified only if it was stated to be present, but not specified to be malignant or benign.
Back to TP, FP, FN. We are dealing with vectors consisting of natural numbers now, rather than binary vectors. Hence we need to redefine these metrics.
Let x be the number of predicted codes within a certain code family f for a document d. Let y be the number of true gold standard codes within the same code family f for a document d.
TP(d, f) = min(x, y)
FP(d, f) = max(x – y, 0)
FN(d, f) = max(y – x, 0)
Where min and max are functions returning the minimum and maximum between two input numbers respectively.
TP represents the numeric overlap, FP and FN represent over-prediction and under-prediction respectively.
Remark: Note that the outputs of the redefined TP, FP, and FN are equivalent to those of their standard definitions assuming binary x and y.
We call this method a Count-Preserving Hierarchical Evaluation (CoPHE).
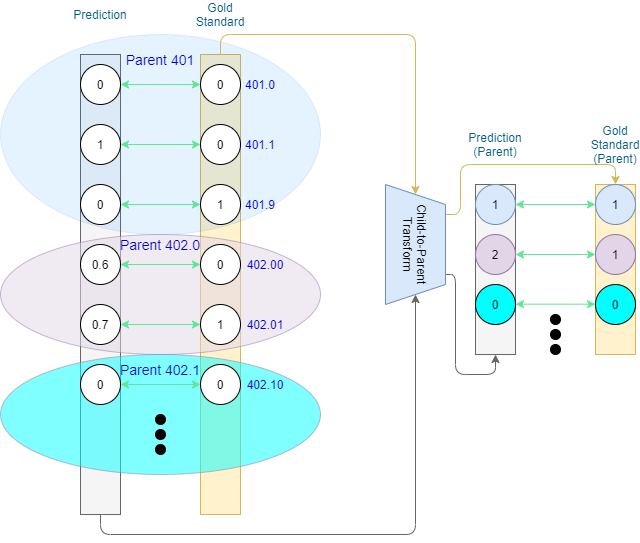
CoPHE is not meant to be used as a replacement of the existing metrics, but rather in tandem with them. In general, hierarchical metrics (set-based and CoPHE) are expected to produce scores mitigating mismatches on the code-level. It is also important to compare set-based hierarchical results to those of CoPHE. Assuming no over-/under-prediction (not captured by the set-based metric) takes place, FN and FP values for CoPHE will stay the same as for set-based, with TP being greater or equal than that of set-based. This would lead to CoPHE Precision, Recall (and consequently F1 score) higher or equal to those of set-based hierarchical evaluation. Should CoPHE results be lower than those of set-based hierarchical evaluation, this is an indication of over-/under-prediction taking place.
We have developed CoPHE for ICD-9 coding and made the code publicly available on Github. The approach can be adjusted to any label-space with an acyclic graph structure. For further details, including results of prior art model on MIMIC-III, please consult the publication.
References
[1] Falis, Matúš, et al. “CoPHE: A Count-Preserving Hierarchical Evaluation Metric in Large-Scale Multi-Label Text Classification.” 2021 Conference on Empirical Methods in Natural Language Processing. 2021.[2]Johnson, Alistair EW, et al. “MIMIC-III, a freely accessible critical care database.” Scientific data 3.1 (2016): 1-9.
[3] Maynard, Diana, Wim Peters, and Yaoyong Li. “Evaluating Evaluation Metrics for Ontology-Based Applications: Infinite Reflection.” LREC. 2008.
[4] Kosmopoulos, Aris, et al. “Evaluation measures for hierarchical classification: a unified view and novel approaches.” Data Mining and Knowledge Discovery 29.3 (2015): 820-865.
